LCM Full Form: In mathematics, LCM stands for “Least Common Multiple,” which is a crucial concept. Understanding the full form of LCM is essential as it plays a significant role in various mathematical operations. Let’s delve deeper into the concept of LCM to gain a comprehensive understanding.
LCM = Least Common Multiple
Other LCM Full Form
| LCM | Least Common Multiple |
| LCM | Lowest Common Multiple |
| LCM | Life Cycle Management |
| LCM | London College of Music |
| LCM | Laser-Capture Microdissection |
| LCM | Lighting Control Module |
| LCM | Liquid Crystal Module |
| LCM | Lymphocytic Choriomeningitis |
| LCM | Leeds College of Music |
| LCM | Long Course Meters |
| LCM | Lower of Cost or Market |
| LCM | Liquid Crystal Display Module |
| LCM | Liquid Composite Molding |
| LCM | Landing Craft, Mechanized |
| LCM | Life Cycle Model |
| LCM | Little Cypress-Mauriceville High School |
| LCM | Life Cycle Manager |
| LCM | Leadership and Change Management |
| LCM | Loss Cost Multiplier |
| LCM | Liquid Composite Molding |
| LCM | Linux Cluster Manager |
| LCM | Lat Computer Manager |
| LCM | Landesk Configuration Manager |
| LCM | Login Client Module |
| LCM | Large Core Memory |
| LCM | Lat Communications Manager |
| LCM | Life Cycle Methodology |
| LCM | Left Click Menu |
| LCM | Lost Circulation Material |
| LCM | Lutheran Church of the Master |
| LCM | Louisiana Children’s Museum |
| LCM | Loss Control Management |
| LCM | Landing Craft Medium |
| LCM | Letalski Center Maribor |
| LCM | Left Costal Margin |
| LCM | Sisters of the Little Company of Mary |
| LCM | Leadership Competency Model |
| LCM | London Canal Museum |
| LCM | Living Computer Museum |
| LCM | Loose Cubic Meter |
| LCM | Life Cycle Monitoring |
| LCM | Leather Case for Motorola |
| LCM | Line Control Module |
| LCM | Large-Capacity Magazine |
| LCM | Lawton Chiles Middle |
| LCM | Local Church Ministry |
| LCM | Large Case Management |
| LCM | Lead Containing Material |
| LCM | Live Current Media |
| LCM | Logistics Cost Management |
| LCM | Live Country Music |
| LCM | Loss Control Manual |
| LCM | Love, Courtship and Marriage |
| LCM | Low Cost Media |
| LCM | Liaison Committee Meeting |
| LCM | Lotsoff Capital Management |
| LCM | Low Cost Move |
| LCM | Legal & Compliance Management |
| LCM | LEAF Creation Method |
| LCM | Laser Countermeasure |
| LCM | Latitude Capital Management |
| LCM | Legal Costs Management |
| LCM | Line Concentrating Module |
| LCM | logical computing machine |
| LCM | Loyal Clan Member |
| LCM | Light Carrying Medium |
| LCM | Logistics Community Manager |
| LCM | Logic Control Module |
| LCM | Line Cost Model |
| LCM | Liquid Cooling Module |
| LCM | Level Converter Module |
| LCM | Launch Confirmation Message |
| LCM | Lens-CCD Module |
| LCM | Locally Corrected Nystrom Method |
| LCM | Lyreco Core Model |
| LCM | Linear Coded Modulation |
| LCM | Line Carrier Module |
| LCM | Lake Champlain and Moriah |
What is LCM? | LCM Full Form
LCM stands for “Least Common Multiple,” which is a concept in mathematics. To understand how to find LCM, it’s important to grasp the concepts of multiples and common multiples first. Once you understand those, you can then proceed to learn how to find the least common multiple.
LEAST COMMON MULTIPLE
Once you’ve grasped the steps mentioned above, determining the Least Common Multiple (LCM) becomes straightforward. Continue reading to understand how to find multiples, identify common multiples, and ultimately calculate the LCM.
Basic Rule Multiple?
Understanding multiples is fundamental to mathematics. Here are some basic rules:
- Every number is a multiple of itself.
- All natural numbers are multiples of 1.
- Multiples of a number are greater than or equal to the number itself.
- There’s no limit to the multiples of a particular number; they are infinite.
- Each number has unlimited multiples.
- There’s no greatest multiple.
- The only way to find multiples is through proper understanding and application of multiplication.
So, before delving into multiples, ensure a solid grasp of multiplication.
How to Find Multiple?
To find the multiples of a number, you multiply that number by 1, 2, 3, 4, and so on. Let’s examine the first few multiples of 4.
| 4 x 1 = 4 |
| 4 x 2 = 8 |
| 4 x 3 = 12 |
| 4 x 4 = 16 |
| 4 x 5 = 20 |
| 4 x 6 = 24 |
| 4 x 7 = 28 |
| 4 x 8 = 32 |
| 4 x 9 = 36 |
| 4 x 10 = 10 |
So, the multiples of 4 are 4, 8, 12, 16, 20, 24, 28, 32, 36, and 40. You can continue this pattern to find more multiples of 4, or any other number.
This is a simple method to find the multiples of any number. Additionally, you can learn how to find the common multiples of different numbers.
How To Find Common Multiples? By Listing Method
To identify common multiples, begin by enumerating the multiples of each number. Then, compare the lists to identify the numbers that appear in both. Let’s demonstrate with the numbers 2 and 3.
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, …
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, …
Now, looking at both lists, we can see that the common multiples of 2 and 3 are 6, 12, 18, 24, …
How To Find Common Multiples by Prime Factorisation?
To find common multiples using prime factorization, you first need to understand prime factorization. Once you’ve grasped that concept, you can easily identify common multiples through this method.
How to Find Prime Factorisation?
Prime factorization of a number occurs when all its factors are prime numbers. There are two methods to determine the prime factorization of any number:
- Factor Tree Method: In this method, you create a tree-like structure, breaking down the number into its prime factors progressively until all factors are prime.
- Common Division Method: With this approach, you repeatedly divide the number by the smallest prime number possible until the quotient is a prime number itself, thus obtaining the prime factorization.
How to Find Prime Factorisation? By Using Factor Tree
Finding the prime factorization of a number using a factor tree is a straightforward process. Follow these steps to easily determine the prime factorization of any given number:
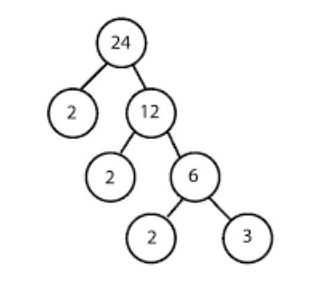
- Begin by identifying the smallest prime factor of the number. For example, let’s take the number 24.
- Divide the number by its smallest prime factor to find the next smaller factor. For 24, the smallest prime factor is 2, so divide 24 by 2 to get 12.
- Repeat the process with the newly obtained factor. Find the smallest prime factor of 12, which is also 2. Divide 12 by 2 to get 6.
- Continue this process until the last row of the factor tree contains only prime numbers.
Using the factor tree method simplifies the process of finding the prime factorization of any number. Now, let’s explore an alternative method for determining prime factorization.
How to Find Prime Factorisation? By Common Division.
To find the prime factorization of a number using the method of common division, start by dividing the number by its smallest prime factors successively until you cannot divide further without getting a prime number. Let’s illustrate this method with an example:

Let’s find the prime factorization of 24.
- Start by dividing 24 by its smallest prime factor, which is 2. 24÷2=12.
- Next, divide 12 by its smallest prime factor, which is 2 again. 12÷2=6.
- Continue dividing 6 by its smallest prime factor, which is 2. 6÷2=3.
- Now, 3 is a prime number, so we stop the division process.
- The prime factorization of 24 is 2×2×2×3
By following this process, you can easily determine the prime factorization of any number. Now, let’s move on to understanding how to find the common multiple.
How to Find Common Multiple? by Prime Factorisation.
To determine the Least Common Multiple (LCM) using prime factorization, you’ll follow a straightforward process. Start by determining the prime factorization of each number. Then, identify the highest power of each prime factor present in either number. Multiply these highest powers together to obtain the LCM. This method ensures you capture all the common factors shared by both numbers.
How To Find The LCM?
LCM stands for Least Common Multiple. There are various methods to find the LCM:
- Listing Multiples Method: List out the multiples of each number and find the smallest number that appears in each list.
- Common Division Method: Divide the numbers by their common factors repeatedly until no more common factors can be divided, then multiply the divisors together.
- Prime Factorization Method: Find the prime factors of each number and then multiply together the highest power of each prime factor that appears in any of the numbers.
- Factor Tree Method: Create a factor tree for each number and then multiply together the prime factors, considering the highest power of each prime factor.
- Division Method: Divide the numbers by the smallest prime numbers, then continue dividing by prime numbers until no more division is possible, then multiply the divisors together.
Each method has its own advantages and may be preferred depending on the numbers involved and personal preference.
How To Find The LCM? by Listing Method
To find the Least Common Multiple (LCM) using the listing method, we first understand that LCM stands for “Least Common Multiple.” By identifying common multiples of the given numbers, we can find their LCM.
Let’s take the numbers 2 and 3. We start by listing their multiples:
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, …
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, …
By comparing these lists, we see the common multiples: 6, 12, 18, 24, …
Tthe LCM of 2 and 3 is 6.
How To Find The LCM? By Common Division Method
To find the LCM (Least Common Multiple) using the Common Division Method, follow these steps:
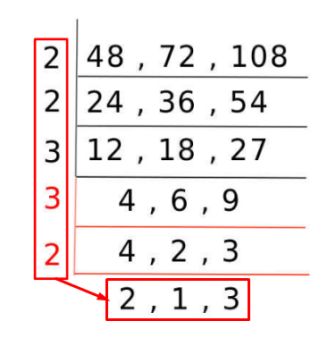
- Begin by listing the numbers whose LCM you want to find. For instance, let’s take 48, 72, and 108.
- Start dividing the numbers by the smallest prime number, which is 2.
- If a number can be divided evenly, write down the divisor and the quotient. If not, carry the number forward.
- Continue this sequence with the next prime number, which is 3.
- Once you’ve exhausted all the prime factors, multiply all the divisors together. This product will be the LCM.
For the example numbers:
48 ÷ 2 = 24
72 ÷ 2 = 36
108 ÷ 2 = 54
24 ÷ 2 = 12
36 ÷ 2 = 18
54 ÷ 2 = 27
12 ÷ 2 = 6
18 ÷ 2 = 9
27 ÷ 3 = 9
6 ÷ 2 = 3
9 ÷ 3 = 3
9 ÷ 3 = 3
3 ÷ 3 = 1
3 ÷ 3 = 1
3 ÷ 3 = 1
Now, multiply all the divisors together:
2 × 2 × 2 × 2 × 3 × 3 × 3 = 432
So, the LCM of 48, 72 and 108 is 432.
How To Find The LCM? by Prime Factorisation Method
Dear friends, In our discussion above, we explored the process of finding common multiples through prime factorization. It’s important to note that you can also determine the Least Common Multiple (LCM) using this method. So, whether you’re utilizing prime factorization or any other method, remember that both approaches can lead you to the LCM. Once again, let’s recall that LCM stands for Least Common Multiple.
Conclusion | LCM Full Form
Friends, let’s delve into the realm of LCM and LCM Full Form. Additionally, learn the art of finding the LCM of any given number. If you notice any issues with this post, feel free to suggest improvements for enhancing its quality. And if you find it informative and engaging, why not share it with your friends?